自主选拔在线团队综合整理“2025清华大学求真书院增设“数学与人工智能硕士项目”并启动招生报名”相关内容，欢迎考生收藏、点阅。

2025清华大学求真书院增设“数学与人工智能硕士项目”并启动招生报名

　　数学是科学的基础

　　也是科技创新的理论根基

　　求真书院秉持数学领军人才培养初心

　　努力在国家亟需的人工智能领域

　　贡献求真力量

2022年7月，求真书院与经济管理学院签署联合培养博士协议，面向数学科学领军人才培养计划学生，探索“数学+经济”顶尖人才贯通培养模式，释放出数学与相关交叉学科联合培养人才的重要信号。

2023年8月，求真书院与自动化系签署联合培养博士协议，面向数学科学领军人才培养计划学生，进一步开启“数学+智能科学”顶尖人才贯通培养新方向。

2023年10月，在与文科、工科交叉合作的基础上，求真书院与生命科学学院签署联合培养博士协议，面向数学科学领军人才培养计划学生，旨在推动完成了数学与文、理、工不同学科代表方向的交叉布局。

　　2024年6月，求真书院与智能产业研究院签署联合培养博士协议，面向书院每年招收的博士研究生，聚焦人工智能学术研究，培养数学与人工智能领域的领军人才。

　　同月，求真书院与自动化系进一步合作，自2024年秋季学期开始，联合设立“数学与人工智能实验班”，开展数学与人工智能交叉的本科人才培养工作。首批实验班学生从2024级自动化大类和求真书院英才班的学生中进行遴选。

　　2024年8月，求真书院进一步完善“数学+人工智能”培养体系，正式设立“数学与人工智能”学术型硕士项目。该项目自2024年秋季开始招生，首届学生将于2025年秋季学期入学。

　　自此，求真书院完成数学与人工智能本科、硕士、博士不同阶段的培养布局，进一步拓宽应用数学领域，助力国家人工智能发展。

　　02/ 数学与人工智能硕士项目详解

　　项目设立初衷

　　Math for AI：数学是人工智能的基础

　　(1)人工智能起源离不开数学家

　　1956 年，约翰·麦卡锡、马文·闵斯基、克劳德·香农等学者(其中众多参与者是数学家，下图紫色框标注)在美国汉诺斯小镇的达特茅斯学院，共同讨论着机器模拟智能的一系列问题。他们讨论了很久，始终没有达成共识，却为讨论内容起了一个名字：人工智能。这个会议就是著名的达特茅斯会议。自此，人工智能(AI，Artificial Intelligence)开始出现在人们的视野，1956 年也就成为了人工智能元年。

　　约翰·麦卡锡(John MacCarthy): 1951年普林斯顿数学博士，图灵奖获得者。在1956年的达特茅斯会议上提出了“人工智能”一词，并被誉为人工智能之父，将数学逻辑应用到了人工智能的早期形成中。

　　马文·闵斯基(Marvin Minsky)：1950年普林斯顿数学博士，图灵奖获得者。1946年进入哈佛大学主修物理，后改学数学，获博士学位。

　　克劳德·香农(Claude Shannon)：1940年MIT数学博士，数学家、密码学家、信息论创始人。

　　雷·所罗门诺夫(Ray Solomonoff)：物理硕士、数学家。机器学习的先驱，算法概率论的创始人，通用概率分布之父，通用归纳推理理论的创建者，奠定人工智能理论的数学基础。

　　奥利弗·塞尔弗里奇(Oliver Selfridge)：1945年MIT数学学士学位，数学家。他是人工智能先驱，被称为机器感知之父。

　　特兰查德·摩尔(Trenchard More)：数学家、计算机科学家。

　　(2)数学(包括基础数学和应用数学)在人工智能领域发挥至关重要的作用

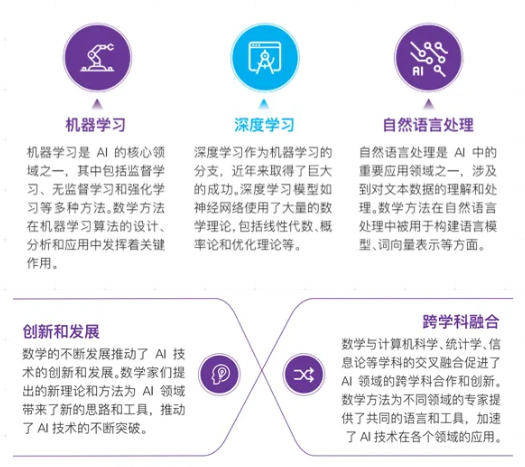
（3）专家视角

　　AI for Math：人工智能推动数学发展

　　数学家在很早就开始利用机械计算辅助进行数学研究。例如，勒让德(Legendre)和高斯(Gauss)利用人力计算完成巨大的素数表，并以此作出关于素数渐进分布的猜想(素数定理)。在电子计算机发明以后，阿佩尔(Appel)和哈肯(Haken)在1970年代利用计算机枚举的方法讨论了一千余种情况，从而证明了关于平面图染色的四色定理。计算机辅助定理证明的早期发展与逻辑学、代数学等数学分支密切相关。例如，华人数学家王浩先生在1950年代至1960年代提出了命题逻辑中的王氏算法，并深远的影响了此后以归结原理(resolution principle)为核心的自动定理证明系统发展;我国数学家吴文俊先生于1970年代提出吴氏方法，将几何问题转化为代数问题，以此通过代数算法完成几何定理的证明。在现代机器学习与人工智能的浪潮下，以Lean为代表的数学定理验证系统为复杂证明提供了严谨的形式化基础，深度和强化学习方法的飞速发展极大的提升了自动定理证明的能力。例如，谷歌DeepMind实验室推出了基于神经符号系统的AlphaGeometry算法将深度神经网络与吴氏方法结合，已经达到了自动求解国际数学奥赛级别的几何问题的水平;在刚刚过去的2024年国际数学奥赛中，DeepMind实验室的增强算法AlphaProof更是完整解决了全部6道题中的4道——该人工智能系统的成绩只差1分就可以达到人类金牌的分数线。未来数学的边界将由数学家与人工智能系统合作开拓。

　　招生培养

　　培养目标：培养具备扎实数学基础，具备在人工智能及相关领域钻研探索精神，且有志于解决国家在人工智能等领域发展的重要问题的优秀人才。

　　招生人数：首年预计招收20人(不含国际生)

　　学位授予：满足培养方案和学位授予要求，授予数学学科理学硕士学位

　　报名方式：符合清华大学2025年接收优秀应届本科毕业生免试攻读研究生的相关规定。具体信息详见清华大学研究生招生信息网址yz.tsinghua.edu.cn。申请人将以下材料在2024年8月23日12:00——9月2日12:00于我校研究生申请服务系统(yzbm.tsinghua.edu.cn)内提交，逾期不予受理。

　　咨询方式：

　　联系电话：010-62783608;

　　电子邮箱：qzsyzs@mail.tsinghua.edu.cn

　　导师团队

　　本项目主要依靠清华大学丘成桐数学科学中心师资(YMSC)和北京雁栖湖应用数学研究院(BIMSA)师资，现有近30人，未来还将继续扩大师资规模。导师团队的研究范围覆盖机器学习理论、自然语言处理、计算机视觉、人工智能赋能自然科学、人工智能系统、统计学、精准医学等关键领域。发表论文绝大多数在国际顶级期刊或顶级会刊上，并在国际学术界产生了重要影响。求真书院院长丘成桐先生不仅在理论数学方面有着全球瞩目的影响力，在应用数学以及交叉学科领域包括人工智能领域也有卓越贡献。例如，丘成桐先生发明的Yau-Yau非线性滤波器方法是新控制论奠基性理论之一;与他学生发明的计算共形几何理论推动了图像技术的飞速发展;与合作者提出的GLMY同调理论，已成为复杂系统与网络解析的最重要的拓扑方法之一;与合作者提出在黎曼流形上重新定义传统PCA的主流形及主边界理论，能挖掘隐藏在数据背后的几何结构，旨在解决传统统计方法和理论中的缺陷。

　　培养特色

　　理论与实践并重：注重数学理论基础与 AI 技术应用相结合，确保学生掌握扎实的数学基础理论，并能应用知识解决实际问题。

　　多学科交叉：AI方向涉及数学、计算机科学、数据科学等多学科，项目强调学科交叉，促进学生综合能力的发展。

　　前沿技术引领：课程设置紧跟AI领域最新发展动态，引入深度学习、 强化学习、自然语言处理等前沿课程，确保学生掌握最新知识。

　　实践驱动学习：通过实践课程，培养学生解决实际问题的能力和创新能力，鼓励学生参与各类 AI 竞赛和科研项目。

　　国际化视野：引入国际前沿教材和课程，鼓励学生参与国际交流与合作，提高学生的国际竞争力。

　　03/ 结语

　　2024年3月，UC伯克利EECS教授Jelani Nelson联合发起了一个倡议，表示支持加州大学BOARS的新规，强调「强大的数学基础对人工智能至关重要」，认为“代数、微积分和概率的核心数学概念是现代AI创新的核心”。在该倡议中，已经有31位知名人物签字，包括马斯克、奥特曼等重要人物以及Open AI、微软、苹果、亚马逊、英伟达、谷歌等重要公司的科学家。

　　https://www.mathmatters.ai/

　　在数学领域，

　　求真书院拥有独一无二的顶尖的师资资源;

　　在人工智能领域，

　　求真书院有能力吸引一大批卓越的人工智能领域学者。

　　期待独一无二你，

　　加入求真，

　　与我们携手，

　　在数学与人工智能领域，

　　走出中国道路，

　　谱写人工智能中国篇章!