2024年第65届国际数学奥林匹克(IMO)于7月15日开幕,7月16日开启考试,考试供分为两天进行,为方便大家了解考试试题及答案,自主选拔在线团队整理了本篇内容,供大家参考!
第四题答案
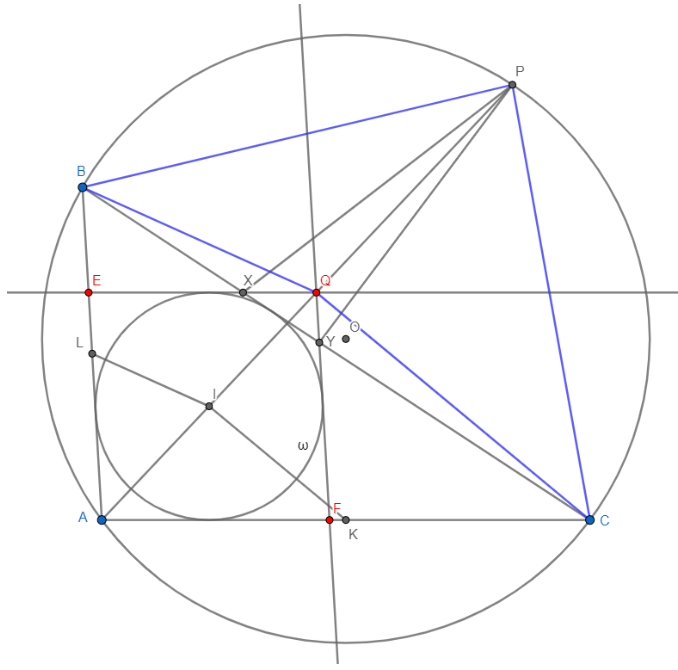
三角形ABC中AB < AC < BC,其内心和内切圆分别为I和ω。X为BC上不同于C的一个点,满足过X平行于AC的直线与ω相切。类似地,Y为BC上不同于B的一个点,满足过Y平行于AB的直线与ω相切。AI再次交三角形ABC的外接圆于P ≠ A,K和L分别为AC和AB的中点。求证:∠KIL +∠YPX = 180˚
这道题的一个显著的着手点是两条平行于三角形两边的切线。不妨把这两条切线延伸开来,与三角形两条边形成一个平行四边形(因为AI是角平行线,实际上形成了一个菱形)。
解答如下:
令过X的ω的切线交AB于E,过Y的ω的切线交AC于F,两条切线相交于Q。
连接BQ、CQ、BP和CP。
因为EQ平行于AC,FQ平行于AB,所以EAFQ是一个平行四边形。同时,该平行四边形的四条边皆为ω的切线,且AI是角平行线,所以EAFQ是一个菱形。
出于对称性,ω的圆心位于该菱形的对角线AQ上,即A、I、Q三点共线,且I为AQ的中点。
因为K为AC的中点,I为AQ的中点,所以KI平行于CQ,∠KIA =∠CQA。
同理,∠LIA =∠BQA。
所以,∠KIL =∠CQB。
因为PCAB四点共圆,∠BCP =∠BAP。
由AB平行于QF,有∠BAP =∠AQY。
所以,∠YCP 与∠YQP互为补角,QYCP四点共圆。
因此,∠YPQ =∠YCQ。
同理,∠XPQ =∠XBQ。
在三角形BCQ中,∠CQB +∠YCQ +∠XBQ = 180°。
所以,∠KIL +∠YPQ +∠XPQ =∠KIL +∠YPX = 180°。证明完毕。
总结:通过平行四边形/菱形找到A关于I的对称点Q是比较明显的,然后利用中线定理将∠KIL平移到∠CQB,最后利用三角形的外接圆和两组平行线证明两组四点共圆,将待证明的三个角移动到同一个三角形内。
第五题答案
蜗牛“透平”在一个2024行、2023列的棋盘上做游戏。棋盘上有2022个格子里藏有怪物。最开始,透平不知道怪物们所在的位置,但他知道除了第一行和最后一行外,每一行都有且只有一个怪物,且每一列最多有一个怪物。从第一行到最后一行,透平进行了一系列的尝试。在每次尝试中,他选择从第一行的任意一个格子出发,不断移动到和当前所在格子具有共同边的相邻格子中。(他也被允许回到之前到达过的格子。)如果他到达了一个里面藏有怪物的格子,他的本次尝试就此结束,他被送回到第一行以重新开始新的尝试。怪物们不会移动,而且透平记住了所有他达到过的格子中是否藏有怪物。如果他到达了最后一行中的任何一个格子,那么他的本次尝试结束,游戏终止。
求正整数n的最小值,使得不论怪物们的位置在哪里,透平都可以通过某个策略确保他最多通过n次尝试就可以到达最后一行。
坦白讲,昨天做这道题时我也没做对,后来经过Ins上的一张图提示才想明白在某个子情况下应该采用的正确策略。
先考虑这个棋盘的行数和列数。棋盘一共有2024行,除去第一行和最后一行,一共还有2022行。此外,棋盘一共有2023列,怪物的数量是2022个,所以,每一行有且只有一个怪物,同时因为每一列最多有一个怪物,因此存在某一列是没有怪物的。
在下面的图示中,我们约定用红色表示蜗牛到达过、且里面藏有怪物的格子;用白色表示蜗牛到达过、且里面没有怪物的格子,或者蜗牛虽然没有到达过、但根据推理可以确认里面没有怪物的格子;用灰色表示蜗牛没有到达过、且不能确认里面是否藏有怪物的格子。
根据题意,第一行和最后一行的格子显然都为白色。
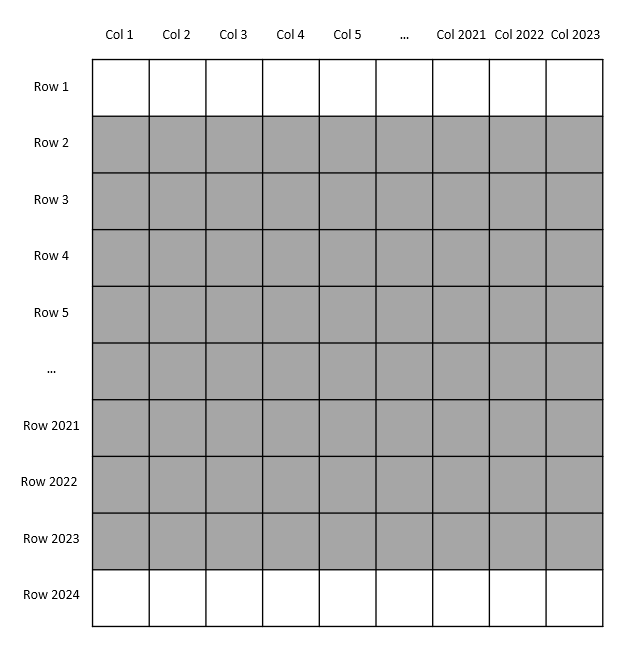
上图是棋盘的起始状态。Row 1和Row 2024分别为第一行和最后一行,这两行的格子里没有怪物。
蜗牛的任务即通过最少次数的尝试,利用每一次尝试结束时确定的红色格子以及它们带来的额外信息,将若干灰色格子转化成红色格子或白色格子,最终形成一条连接第一行和最后一行的白色格子通道,使得它在最后一次尝试中沿着这条白色通道顺利完成游戏。
现在考虑蜗牛在某次尝试的某个格子里,比如Row 3/Col 5里碰到了怪物。
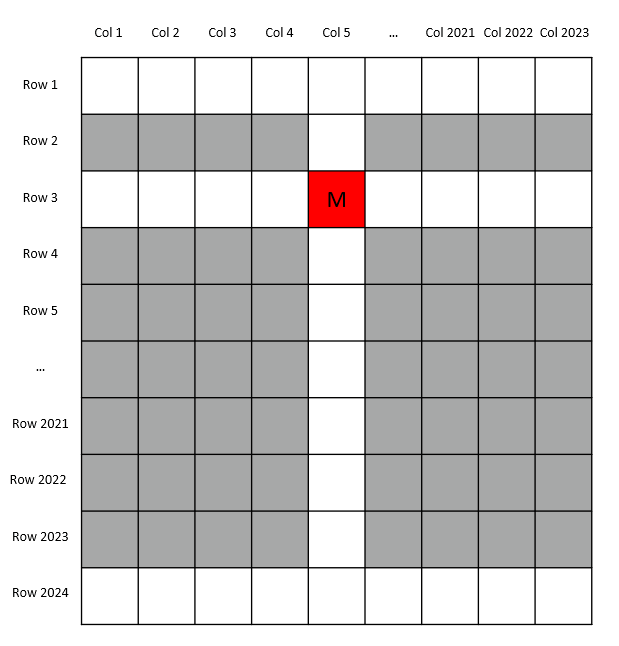
那么根据题意,蜗牛可以判断出在Row 3和Col 5的其他格子里不会再有怪物。此时,我们发现怪物的格子与最后一行之间的所有格子都是白色,换句话说,如果蜗牛在下一次尝试中能够到达红色格子下方的那个格子,即Row 4/Col 5,那么它可以选择一直往下,顺利畅通地抵达最后一行。
因此,问题在于,如何能够用最少的尝试次数到达红色格子下方的那个格子?
以上图为例,要到达Row 4/Col 5,蜗牛需要两次穿过灰色的未知区域,即从Row 2/Col 5到达Row 3的某个白色格子,再从Row 3的那个白色格子到达Row 4/Col 5。
但是,如果这个红色格子在第二行的话,那么蜗牛将省去第一次穿过灰色区域的必要,因为它可以从第一行直接进入第二行。
因此,蜗牛的第一次尝试可以用来找出第一行藏有怪物的那个红色格子。
这个目的很容易实现:蜗牛可以从第一行进入Row 2/Col 1,然后在第二行横向移动,直到碰到怪物,从而确定第二行红色格子的位置。因为第二行中有、且只有一个怪物,所以蜗牛的第一次尝试必然在第二行结束。
蜗牛第一次尝试的结果可能有两种:
1. 第二行的红色格子位于第k列,2 ≤ k ≤ 2022。即怪物藏在除第一列和最后一列以外的某一列,例如Row 2/Col 4。
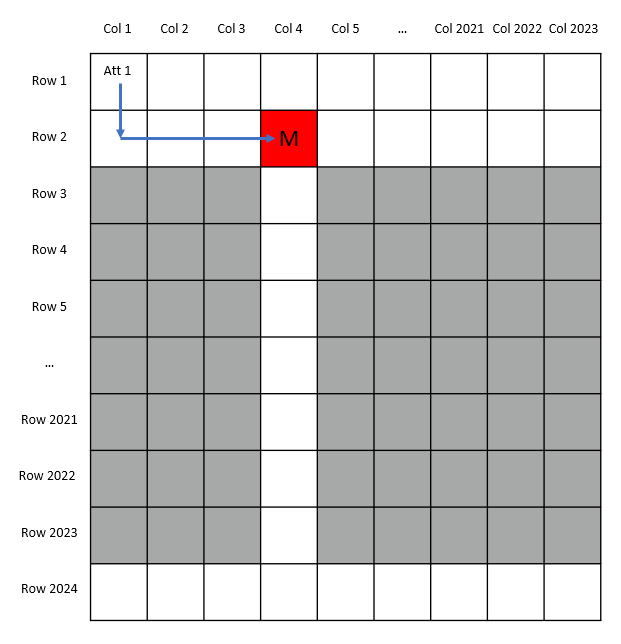
在这种情况下,蜗牛需要利用第二次尝试来找到从Row 2到达红色格子下方格子的路线。
类似地,蜗牛可以从Row 2/Col 1进入Row 3/Col 1,然后在第三行横向移动,直到碰到怪物,从而确定第三行红色格子的位置。
不论第三行红色格子位于第二行红色格子的左下侧,还是右下侧,在第三次尝试中,蜗牛都可以相应地找到某条路径,该路径从第二行红色格子的右下侧或者左下侧进入第三行的白色格子,进而顺着第二行红色格子下方的通道直达最后一行。如下图所示。
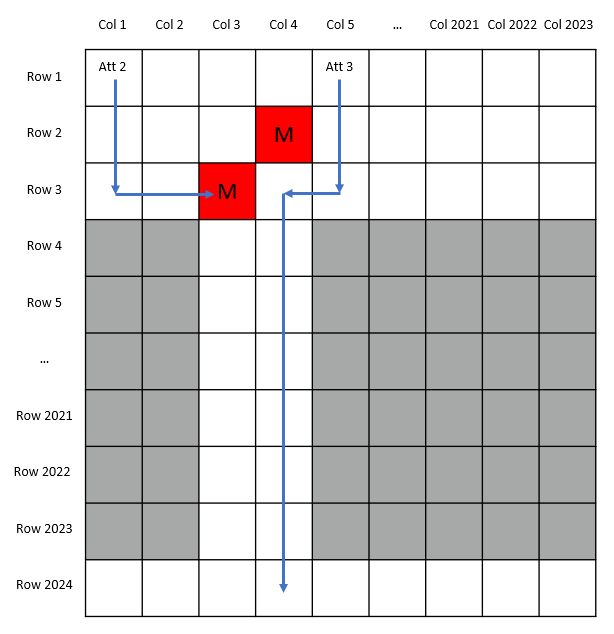
2. 第二行的红色格子位于第一列或最后一列。
出于对称性,我们假设红色格子位于第一列。如果红色格子位于最后一列,蜗牛将移动的策略进行水平翻转即可。
此时如果蜗牛采用和第一种情况相同的策略,即在第二次尝试中遍历第三行找出红色格子,那么运气不好的话,第三行的红色格子可能出现在Row 3/Col 2,如下图所示,此时蜗牛无法找到通往两个红色格子下方由白色格子组成的通道的路径。
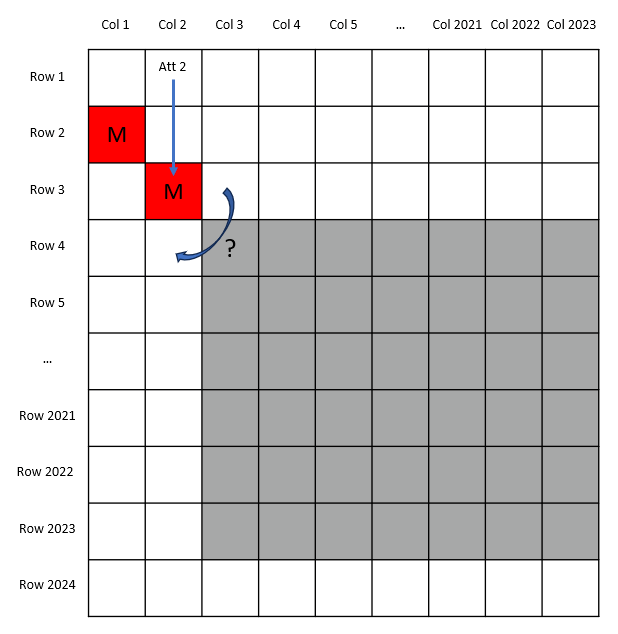
因此,在这种情况下,蜗牛需要采取另一种策略。
考虑最坏的情况:如果所有的2022个怪物都藏在从Row 2/Col 1到Row 2023/Col 2022的直线上,那么Row 2023/Col 2023必然是一个白色格子,蜗牛可以通过那个格子进入到最后一行。
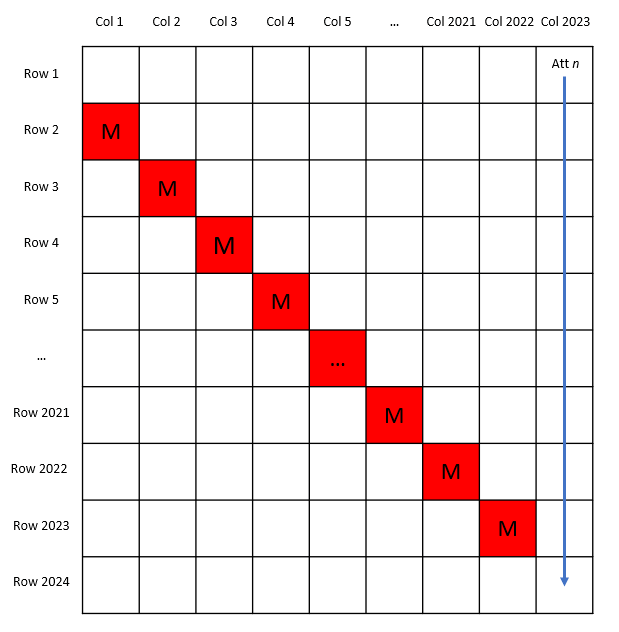
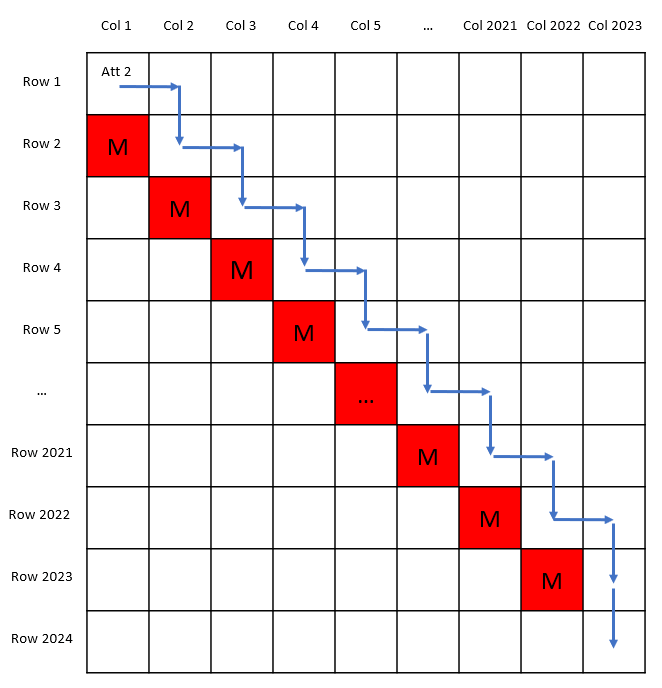
2.1 在最坏的情况下,如果蜗牛“贴着”这条对角线、以“Z”字形方式移动,即沿着如下路线:
Row 1/Col 1 -> Row 1/Col 2 -> Row 2/Col 2 -> Row 2/Col 3 -> … -> Row 2022/Col 2022 -> Row 2022/Col 2023 ->Row 2023/Col 2023
或者:Row i/Col i -> Row i/Col (i + 1) -> Row (i + 1)/Col (i + 1) …,其中1 ≤ i ≤ 2022
那么它就可以顺利到达最后一行的Row 2024/Col 2023(这个策略我之前没有想到!)
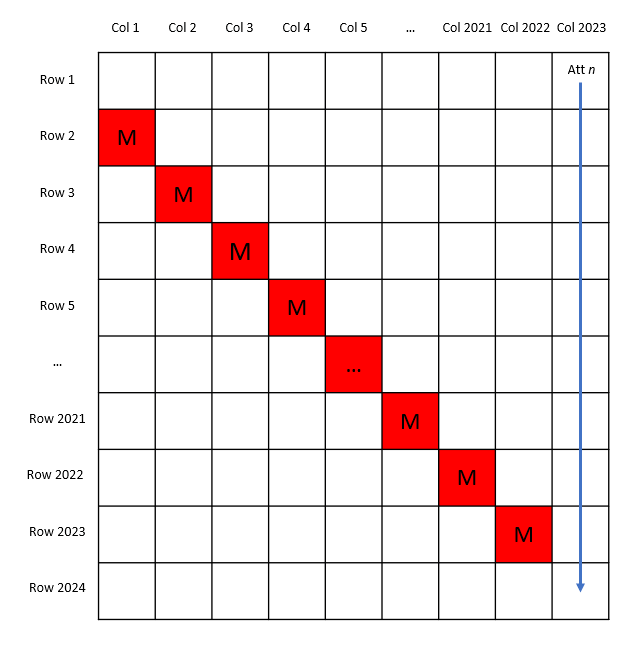
2.2 如果蜗牛在这条路线的途中“不幸”碰到怪物,例如在Row i/Coli或者Row i/Col (i + 1)处出现红色格子,如下图所示:
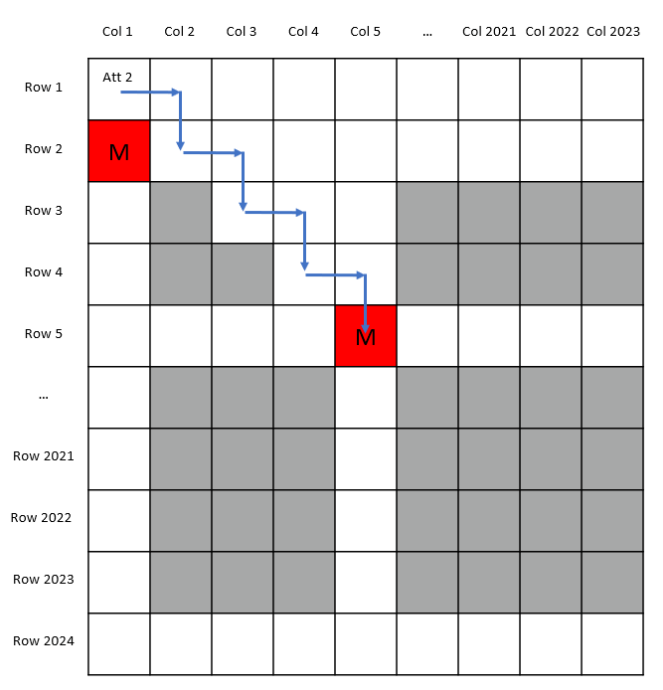
考虑到在第i行,这个红色格子左侧所有的格子必然都是白色。这些格子中包含Row 2/Col 1下方的白色格子Row i/Col 1,且红色格子左邻的白色格子Row i/Col (i – 1)或者Row i/Col i必然与蜗牛两步之前到达的那个白色格子Row (i – 1)/Col (i – 1)或Row (i – 1)/Col i相连,从而形成了一条白色的通道,蜗牛可以在第三次尝试中沿着这条通道顺利到达最后一行。
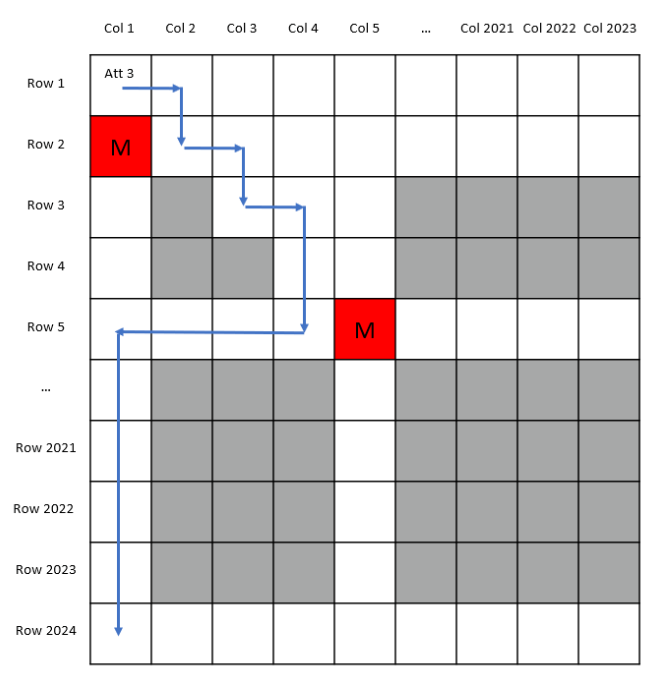
综上,蜗牛最多在3次尝试之后,就可以确保到达最后一行。
同时,找到一个红色格子最少需要1次尝试(因为碰到红色格子该次尝试就结束了),找到从第一行白色格子区域穿过灰色区域进入红色格子下方的白色通道最少需要1次尝试,最后蜗牛沿着已知的通道从第一行到达最后一行需要1次尝试,因此,蜗牛最少需要3次才能完成这个任务。
结合以上两个结论,n的最小值等于3。
总结:这是一道非常有意思的智力题,或者说,是一道更像OI考题的MO考题,拍脑袋估计双料选手们在这道题上的得分会比较高?成绩公布后如果有时间我会统计一下。
第六题答案

温馨提示:为方便大家交流联系,欢迎大家扫描下方二维码加入"2025强基综合评价交流群",我们有专业的老师将为大家线上答疑。
扫一扫即可进群
如果加群失败,可在企业微信联系人中 添加青桐老师(微信号:15321584635)好友,备注:省市-高考年份。

























px.png)












